区间DP详解

区间DP详解

doooge

·

2025-05-13 00:04:49

·

算法·理论

哈喽大家好，我是 doooge，今天给大家带来的是 区间DP 的详解。

\Huge \sf 区间DP 详解

1.什么是区间DP

区间DP 是动态规划的一部分。

1.1 dp_{i,j} 的含义

所谓 区间DP，也就是 dp 数组 dp_{i,j} 表示的是一个区间的答案，比如说 dp_{2,5} 表示的就是 [2,5] 这个区间的答案，dp_{3,7} 表示的就是 [3,7] 这个区间的答案。

而且，dp_{i,j} 只能由它的子区间转移而来，也就像下图这样：

是不是很简单？那我们应该用怎样的顺序去遍历 i,j 使得在 [i,j] 的子区间一定在遍历到 [i,j] 前全部推完呢？

1.2 区间DP的遍历方式

我们可以枚举长度遍历。比如说，我们在遍历到 i,j 时，长度在 j-i+1 以下的区间一定会被遍历掉，可以看下图理解：

遍历的代码也很好写：

for(int l=1;l<=n;l++){//遍历长度

for(int i=1;i<=n-l+1;i++){//枚举左端点

int j=i+l-1;//求出右端点

//dp[i][j]=...

}

}

1.3 DP推出的结果在哪

这个其实很好猜，根据我们以往的经验，一维 dp 的答案一般是最后遍历到的第 n 位 dp_n，那么区间DP 的答案应该就是我们最后遍历到的区间，也就是长度最长的区间 dp_{1,n} 这里。

当然，也有特例，当题目要你求所有状态之和时，这时答案就不太可能是 dp_{1,n} 了，而是每个区间的答案之和，用公式表达就是：

\sum_{l=1}^{n} \sum_{i=1}^{n-l+1} dp_{i,i+l-1}

也可以是：

\sum_{i=1}^{n} \sum_{j=i+1}^{n} dp_{i,j}

当然这两个求和公式的本质都是一样的，遍历每个区间，只是遍历方式的不同而已。

2.区间dp的例题

2.1 T1:P1775 石子合并（弱化版）

有 N 堆石子排成一排，每堆石子有一定的质量 m_i。现在要将这 N 堆石子合并成为一堆。每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，合并后与这两堆石子相邻的石子将和新堆相邻。试找出一种合理的方法，使总的代价最小，并输出最小代价。

### 2.1.1 思路：

我们先把样例搬过来模拟一下：

**输入 #1**

```

4

2 5 3 1

```

**输出 #1**

```

22

```

我们可以按以下顺序合并：


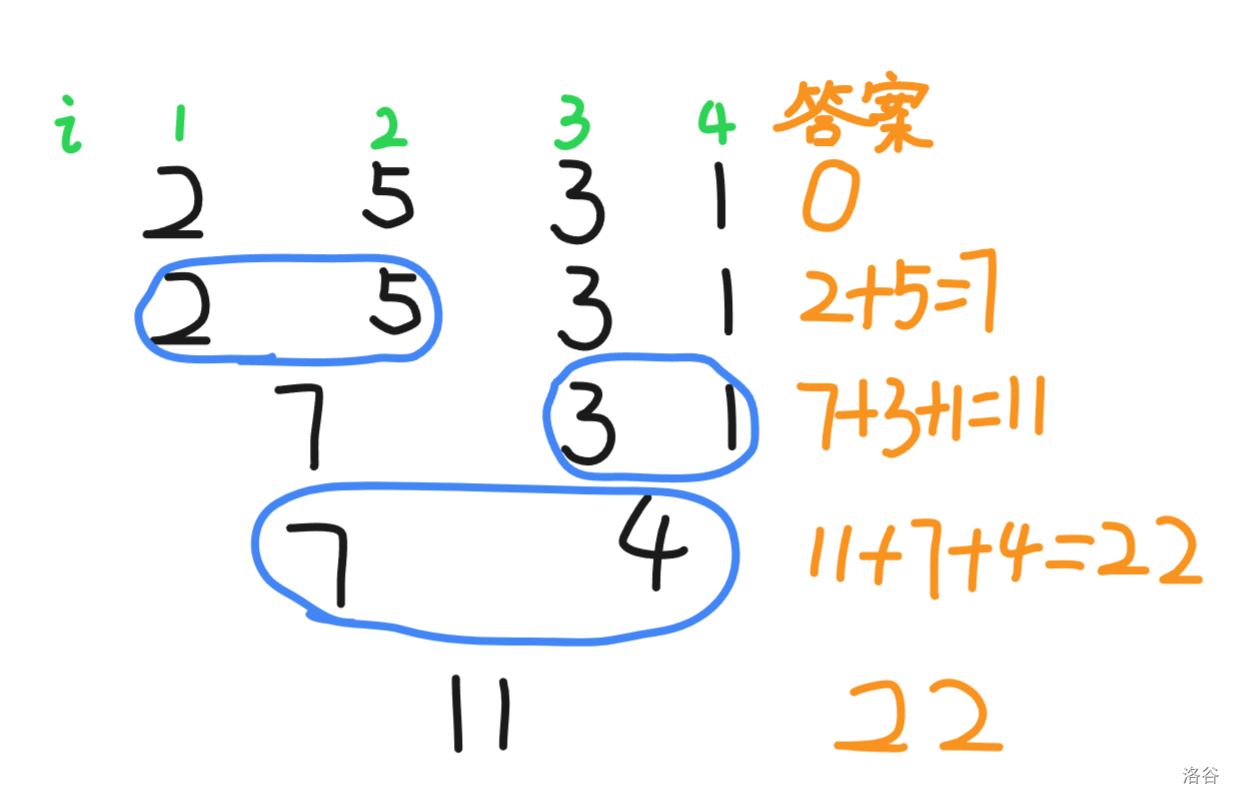
我们发现，不管怎么合并，$[i,j]$ 合并出来的石子堆的大小都是一样的，也就是，不管怎么合并，这一步合并的方法跟后续的合并没有影响。

比如说，这里有四堆石子 $a,b,c,d$，我们用两个方法先合并 $b,c,d$ 这 $3$ 堆石子，再去合并第 $4$ 堆石子 $a$，情况是这样的：



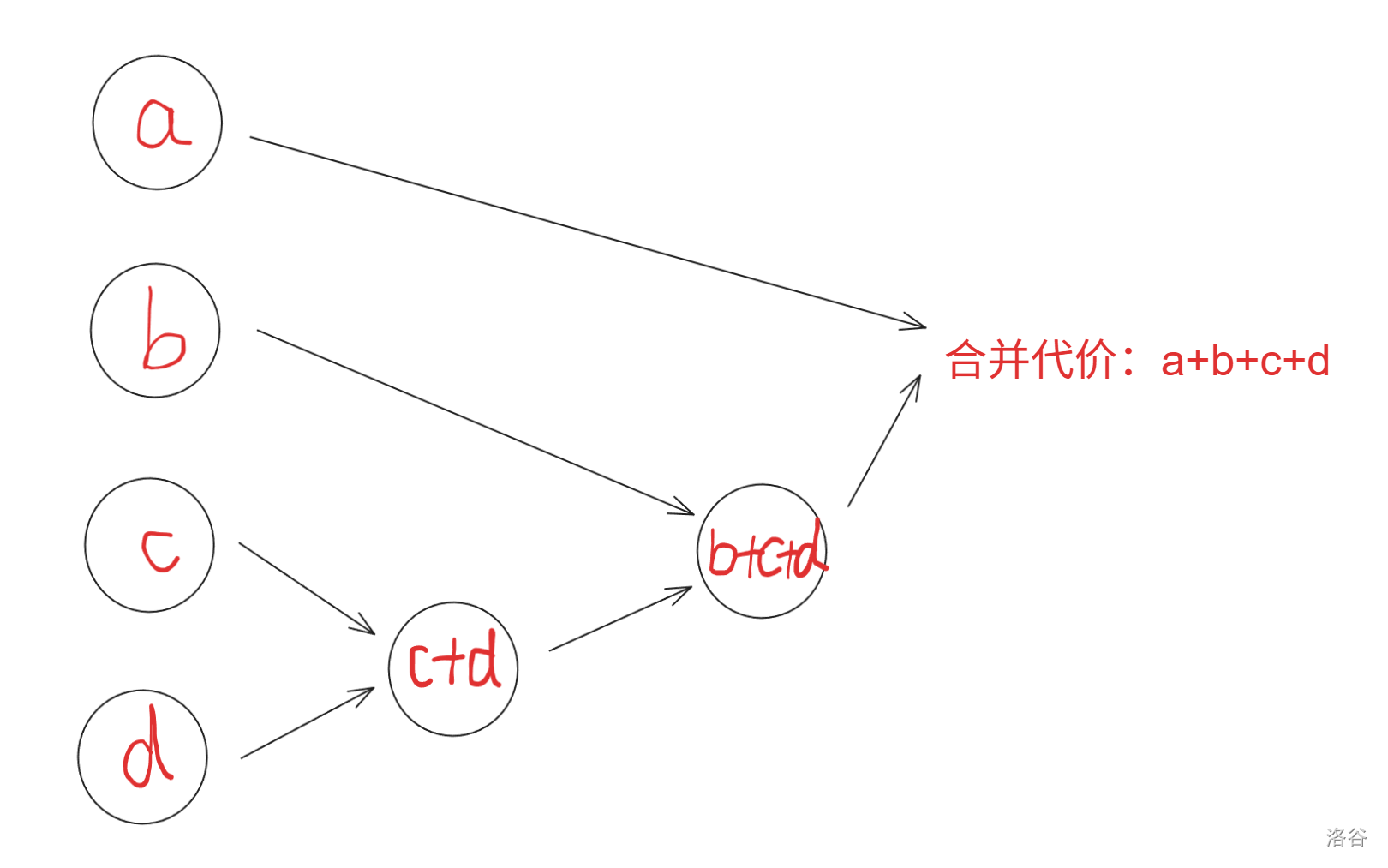
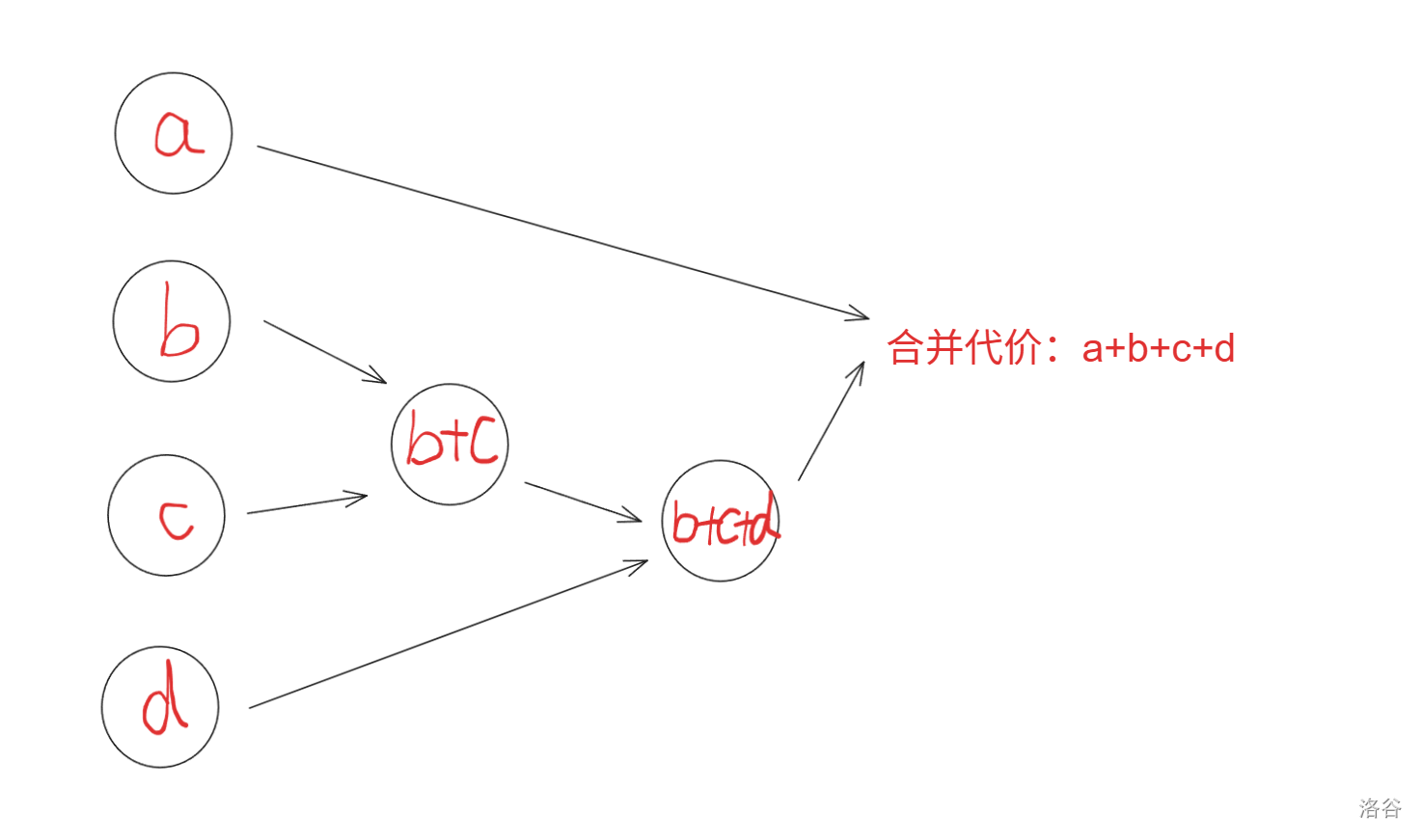
于是！我们就可以用 $dp_{i,j}$ 表示合并 $[i,j]$ 这几堆石子合并到一起所需的最小代价。那么我们最后的答案就是 $dp_{1,n}$ 了。

那我们的 $dp_{i,j}$ 应该从哪里转移过来呢？我们可以想象 $[i,j]$ 这堆石子怎么合并过来的。

诶！我们发现，$[i,j]$ 这堆石子是通过包含在 $[i,j]$ 里面的两小堆石子合并而来的，那么我们的 $dp_{i,j}$ 应该也是找一个断点 $k$，从 $dp_{i,k}$ 和 $dp_{k+1,j}$ 再加上合并的代价得到的，也就是这样：


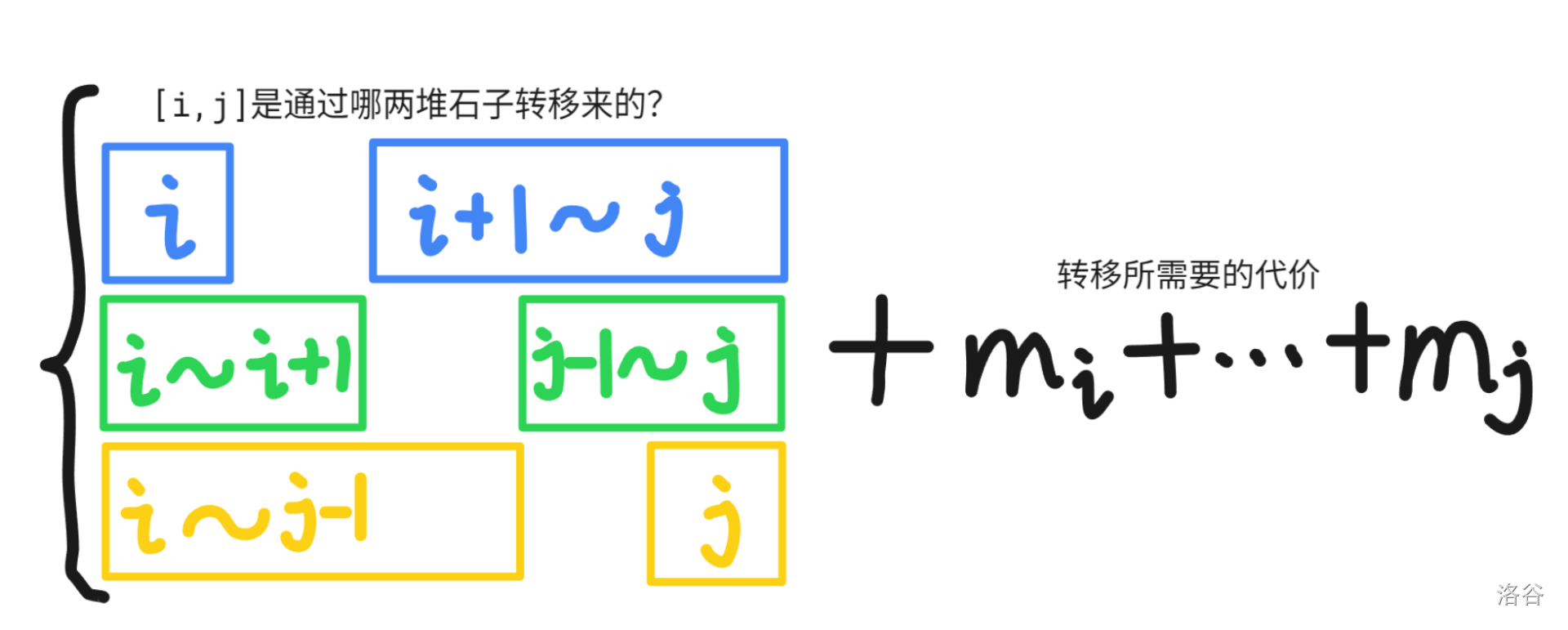
而 $m_i + m_{i+1} + \cdots + m_j$ 可以用前缀和记录（记为 $s$ 数组），于是 $dp_{i,j}$ 就等于：

$$

\min_{k=i}^{j-1} dp_{i,k}+dp_{k+1,j}+s_j-s_{i-1}

$$

转移代码：

```cpp

for(int k=i;k

dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+s[j]-s[i-1]);

}

```

而当长度为 $1$ 的区间由于不需要转移，$dp_{i,i}$ 本来就是 $0$（因为不用合并），所以我们枚举长度 $l$ 的时候直接从 $2$ 开始枚举。

**注意：由于求的是最小代价，所以要将 $dp_{i,j}$ 在转移前初始化为极大值。**

求 $dp$ 数组的代码：

```cpp

for(int l=2;l<=n;l++){//枚举长度

for(int i=1;i<=n-l+1;i++){//枚举起点

int j=i+l-1;//根据起点和长度求出终点

dp[i][j]=1e9;//转移前先初始化成极大值

for(int k=i;k

dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+s[j]-s[i-1]);//转移方程如上文所述

}

}

}

```

求 $dp$ 数组的代码已经出来了，那么完整代码也一定不难了吧！

## 2.1.2

代码（已压行）：

```cpp

#include

using namespace std;

int s[310],dp[310][310];

int main(){

int n;

cin>>n;

for(int i=1;i<=n;i++){

int x;

cin>>x;

s[i]=s[i-1]+x,dp[i][i]=0;

}

for(int l=2;l<=n;l++)for(int i=1;i<=n-l+1;i++){

int j=i+l-1;

dp[i][j]=1e9;

for(int k=i;k

}

cout<

return 0;

}

```

时间复杂度：$O(n^3)$。

## 2.2 [P1435 [IOI 2000] 回文字串](https://www.luogu.com.cn/problem/P1435)

回文词是一种对称的字符串。任意给定一个字符串，通过插入若干字符，都可以变成回文词。此题的任务是，求出将给定字符串变成回文词所需要插入的最少字符数。

比如 $\verb!Ab3bd!$ 插入 $2$ 个字符后可以变成回文词 $\verb!dAb3bAd!$ 或 $\verb!Adb3bdA!$，但是插入少于 $2$ 个的字符无法变成回文词。

**注意**：此问题区分大小写。

记字符串长度为 $l$，$1 \le l \le 1000$。

### 2.2.1 思路

你没听错，这确实是一道 IOI 的题。

咳咳，不扯那么多，我直接来讲这道题用 区间DP 怎么做。

这个时候，聪明的读者就会说了：诶！这题我会！$dp_{i,j}$ 表示让 $s$ 的子串 $s_i$ 到 $s_j$ 变成回文字符串所需要最少的插入字符数。而答案，就是 $dp_{1,n}$ 啦！

那我们的 $dp_{i,j}$ 应该从哪里转移而来呢？可以看下图理解：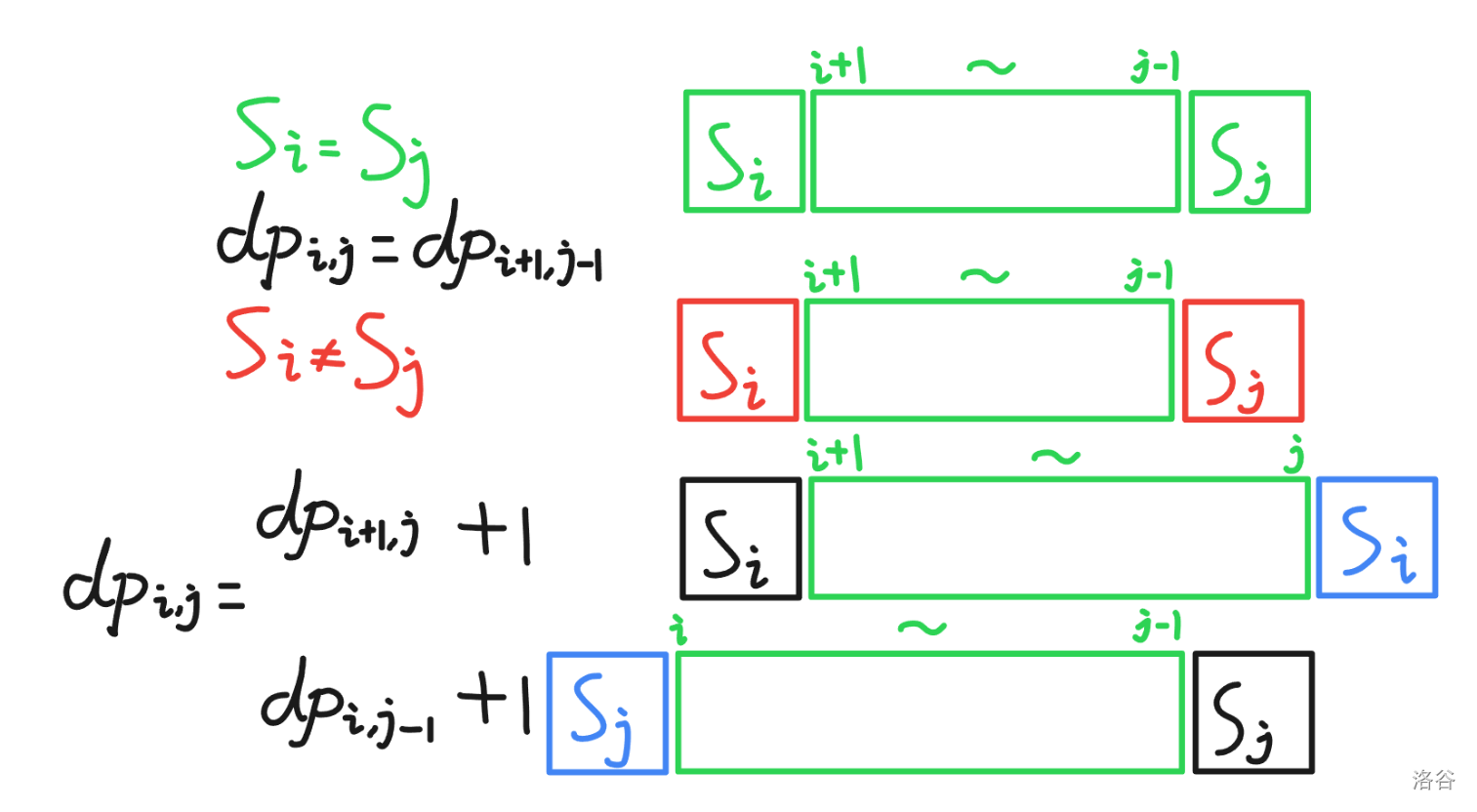


- 如果 $s_i=s_j$ 的话，$dp_{i,j}$ 可以从 $dp_{i+1,j-1}$ 转移过来。

- 否则，我们可以从 $dp_{i+1,j}$ 转移过来并在字符串后面添加一个 $s_i$ 来保持字符串回文，也可以从 $dp_{i,j-1}$ 转移过来并在字符串前面添加一个 $s_j$ 来保持字符串回文。由于我们要求最小长度，应该将前两者取最小值作为答案。

转移代码：

```cpp

if(s[i]!=s[j]){//如果不相等

dp[i][j]=min(dp[i][j-1],dp[i+1][j])+1;

}

else{//否则直接从dp[i+1][j-1]转移而来

dp[i][j]=dp[i+1][j-1];

}

```

与上一题一样，长度为 $1$ 的区间不用转移，因为 $1$ 个字符组成的字符串一定是回文的字符串。而长度为 $2$ 的区间可以特殊处理，但是并没有必要，因为只有 $s_i=s_j$ 的情况才可能越界导致访问到 $dp_{i,i+1}$ 这样长度为 $0$ 的区间，但是我们可以将它初始化为 $0$，这样就不用特殊处理了。

**注意：与上题一样，由于求的是最小代价，所以要将 $dp_{i,j}$ 在转移前初始化为极大值。**

### 2.2.2 代码

代码（已压行）：

```cpp

#include

using namespace std;

int dp[1010][1010];

int main(){

string s;

cin>>s;

for(int l=2;l<=s.size();l++)for(int i=0;i<=s.size()-l;i++){

int j=i+l-1;

if(s[i]!=s[j])dp[i][j]=min(dp[i][j-1],dp[i+1][j])+1;

else dp[i][j]=dp[i+1][j-1];

}

cout<

return 0;

}

```

时间复杂度：$O(n^2)$。

# 3.区间DP 的经典套路题

接下来的题目是 区间DP 的经典套路题，许多 区间DP 题都有这些题的套路。

## 3.1 [P1880 [NOI1995] 石子合并](https://www.luogu.com.cn/problem/P1880)

在一个圆形操场的四周摆放 $N$ 堆石子，现要将石子有次序地合并成一堆，规定每次只能选相邻的 $2$ 堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。

试设计出一个算法,计算出将 $N$ 堆石子合并成 $1$ 堆的最小得分和最大得分。

$N \le 200$。

## 3.1.1 思路

这道题和石子合并唯一的区别就是石子是环形排列。那我们应该怎样解决呢？

我们可以考虑一下环形合并带来的影响。

我们先画一个环：

![](https://cdn.luogu.com.cn/upload/image_hosting/b6zmp01b.png?x-oss-process=image/resize,m_lfit,h_200,w_200

)

我们考虑可能会跨界（也就包括 $5$ 的石子堆合并到包括 $1$ 的石子堆的情况，有以下几种：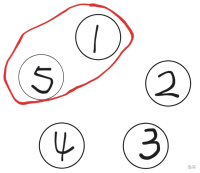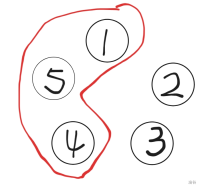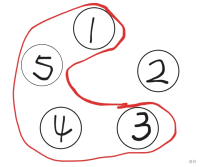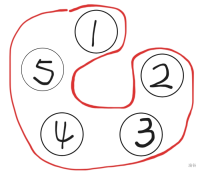

![](https://cdn.luogu.com.cn/upload/image_hosting/wjx6kf3k.png?x-oss-process=image/resize,m_lfit,h_200,w_200

)





这五种合并方式会导致越界。

那我们应该如何解决越界的情况呢？如果我们把一个合并的环环拉成一条线的话：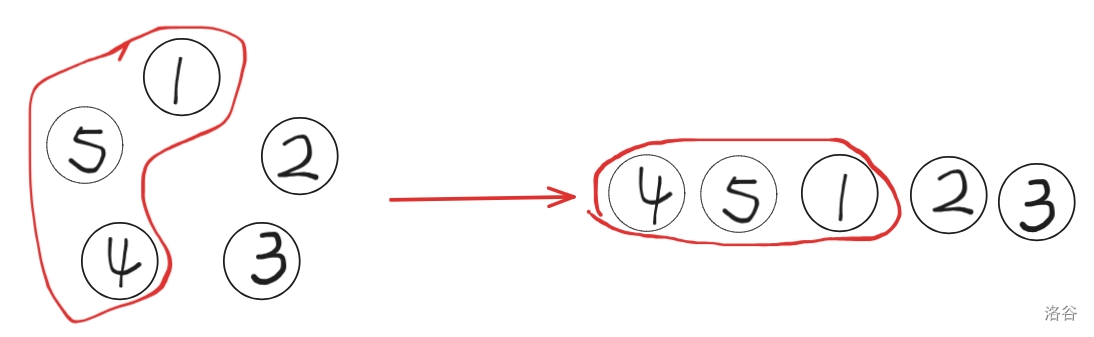


发现了吗！如果我们把整个 $1 \thicksim n$ 的数组复制两边，再把区间长度限制到 $n$ 的话，就能解决环形的问题了：


所以！代码也就很简单了！

### 3.1.2 代码

代码：

```cpp

#include

using namespace std;

int dp[210][210],dp2[210][210],a[210],s[210];

int main(){

int n,ans1=1e9,ans2=-1e9;

cin>>n;

for(int i=1;i<=n;i++){

cin>>a[i];

s[i]=s[i-1]+a[i];//前缀和

a[n+i]=a[i];//求n+1到2n的a数组

}

for(int i=n+1;i<=2*n;i++){//求n+1到2n的前缀和

s[i]=s[i-1]+a[i-n];

}

for(int l=2;l<=n;l++){//长度最大只有n

for (int i=1;i<=2*n-l+1;i++){

int j=i+l-1;

dp[i][j]=1e9;//求最小值

for (int k=i;k<=j-1;k++){//同石子合并弱化版

dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]);

}

dp[i][j]+=s[j]-s[i-1];

}

}

for(int l=2;l<=n;l++){//求最大值

for(int i=1;i<=2*n-l+1;i++){

int j=i+l-1;

for(int k=i;k<=j-1;k++){

dp2[i][j]=max(dp2[i][j],dp2[i][k]+dp2[k+1][j]);

}

dp2[i][j]+=s[j]-s[i-1];

}

}

for(int i=1;i<=n;i++){//找答案

ans1=min(ans1,dp[i][n+i-1]);

ans2=max(ans2,dp2[i][n+i-1]);

}

cout<

return 0;

}

```

## 3.2 [[NOIP 2003 提高组] 加分二叉树](https://www.luogu.com.cn/problem/P1040)

设一个 $n$ 个节点的二叉树 $\text{tree}$ 的中序遍历为$(1,2,3,\ldots,n)$，其中数字 $1,2,3,\ldots,n$ 为节点编号。每个节点都有一个分数（均为正整数），记第 $i$ 个节点的分数为 $d_i$，$\text{tree}$ 及它的每个子树都有一个加分，任一棵子树 $\text{subtree}$（也包含 $\text{tree}$ 本身）的加分计算方法如下：

$\text{subtree}$ 的左子树的加分 $\times$ $\text{subtree}$ 的右子树的加分 $+$ $\text{subtree}$ 的根的分数。

若某个子树为空，规定其加分为 $1$，叶子的加分就是叶节点本身的分数。不考虑它的空子树。

试求一棵符合中序遍历为 $(1,2,3,\ldots,n)$ 且加分最高的二叉树 $\text{tree}$。要求输出

1. $\text{tree}$ 的最高加分。

2. $\text{tree}$ 的前序遍历。

$1 \le n < 30$。

### 3.2.1 思路

这道题一眼看上去并不是 区间DP，其实不然。

题目要求我们建立一颗中序遍历为 $1,2,\cdots,n$ 的树，我们可以看看中序遍历为 $1,2,\cdots,n$ 的树有什么性质。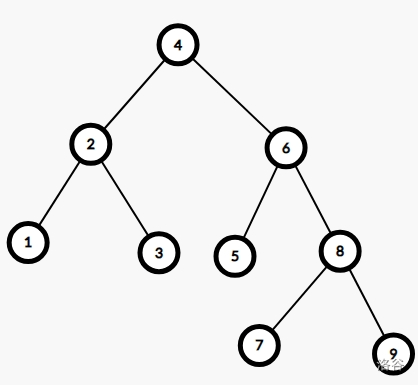


我们发现，每一个节点的左儿子的编号都会小于本节点的编号，每一个节点的右儿子的编号都会大于本节点的编号。于是，$dp_{i,j}$ 就能表示 $i$ 到 $j$ 的节点按中序遍历的顺序为 $i,i+1,\cdots,j$ 所得到的树的最大得分。

$dp_{i,j}$ 怎么转移呢？我们可以看看上面的图片。

我们可以发现，在 $i,j$ 区间内建成的树，如果让 $k$ 作为根，那么这两个子树一定就是 $i,k-1$ 和 $k+1,j$，得分就是 $dp_{i,k-1} \times dp_{k+1,j}+d_k$。我们只要取最大值就行了。

所以转移代码就是：

```cpp

for(int k=i+1;k

if(dp[i][k-1]*dp[k+1][j]+a[k]>dp[i][j]){

dp[i][j]=dp[i][k-1]*dp[k+1][j]+a[k];

}

}

```

但是，如果区间长度为 $2$，此时必然只有一个子树，但题目中说了 `若某个子树为空，规定其加分为 1`，于是我们就可以加一个 `while` 特判。

那我们应该如何输出最终的建成的树呢？我们可以建立一个前驱数组 $fa$，$fa_{i,j}$ 表示 $i,j$ 这棵树是的根是 $fa_{i,j}$，也就是把这棵树分成了 $i,fa_{i,j}-1$，$fa_{i,j}+1,j$ 这两个部分，然后递归求解。

题目要求前序输出这棵树，我们就可以先输出这棵树的根 $fa_{i,j}$，然后在 DFS 递归 $i,fa_{i,j}-1$ 和 $fa_{i,j}+1,j$ 这两棵子树，如果 $i=j$ 就代表递归到叶子结点了，直接输出 $i$ 即可。

输出代码：

```cpp

void print(int l,int r){

if(l==r){//如果是叶子节点

cout<

return;

}

cout<

if(fa[l][r]!=l)print(l,fa[l][r]-1);//递归左节点

if(fa[l][r]!=r)print(fa[l][r]+1,r);//递归右节点

return;

}

```

于是！这道题基本上就解决了！

### 3.2.2 代码

代码（已压行）：

```cpp

#include

using namespace std;

int a[50],dp[50][50],fa[50][50];

void print(int l,int r){

if(l==r){

cout<

return;

}

cout<

if(fa[l][r]!=l)print(l,fa[l][r]-1);

if(fa[l][r]!=r)print(fa[l][r]+1,r);

return;

}

int main(){

int n;

cin>>n;

for(int i=1;i<=n;i++)cin>>a[i],dp[i][i]=a[i],fa[i][i]=i;

for(int l=2;l<=n;l++)for(int i=1;i<=n-l+1;i++){

int j=i+l-1;

dp[i][j]=max(dp[i+1][j]+a[i],dp[i][j-1]+a[j]);

fa[i][j]=(dp[i+1][j]>dp[i][j-1]?i:j);

for(int k=i+1;kdp[i][j]){

dp[i][j]=dp[i][k-1]*dp[k+1][j]+a[k];

fa[i][j]=k;

}

}

cout<

print(1,n);

return 0;

}

```

## 3.3 关路灯

某一村庄在一条路线上安装了 $n$ 盏路灯，每盏灯的功率有大有小（即同一段时间内消耗的电量有多有少）。老张就住在这条路中间某一路灯旁，他有一项工作就是每天早上天亮时一盏一盏地关掉这些路灯。

为了给村里节省电费，老张记录下了每盏路灯的位置和功率，他每次关灯时也都是尽快地去关，但是老张不知道怎样去关灯才能够最节省电。他每天都是在天亮时首先关掉自己所处位置的路灯，然后可以向左也可以向右去关灯。

现在已知老张走的速度为 $1m/s$，每个路灯的位置（是一个整数，即距路线起点的距离，单位：$m$）、功率（$W$），老张关灯所用的时间很短而可以忽略不计。

请你为老张编一程序来安排关灯的顺序，使从老张开始关灯时刻算起所有灯消耗电最少（灯关掉后便不再消耗电了）。

$1 \le n \le 200$。

### 3.3.1 思路

我们知道老张关灯的时间不计，那么如果有一连串的灯，他应该全部关掉，如下图：


如果我们只关掉了部分的灯，那么为了关掉剩余的灯，我们就要折返重新关掉一遍，这样就多出来两站灯的功耗，所以这样肯定不是最优的。

我们还可以发现，如果把一条路径上的灯全关掉，关掉会形成一个区间。于是，我们可以用 区间DP 来解决这道题，$dp_{i,j}$ 表示关掉 $i,j$ 区间的灯所需要的最小功耗。

那么我们应该怎样计算功耗呢？请看下图：


相信大家应该都懂了吧。那 $dp_{i,j}$ 应该从哪里转移而来呢？这似乎成了个问题，因为我们不知道关完 $i,j$ 的灯后我们在哪里。


现在面临着两个选择：

1. 增加一个维度表示位置，但是前面的推论可能推倒重来

2. 直接不演了 

额...还是选 $1$ 吧。我们考虑多加一个维度 $dp_{i,j,0}$ 或 $dp_{i,j,1}$ 表示关完 $i,j$ 区间的灯最后停在左边或停在右边的答案。这样转移就好写多了：

我们先考虑 $dp_{i,j,0}$，也就是关完 $i,j$ 的灯停在左边的转移。


不难看出，$dp_{i,j,0}$ 是由 $dp_{i+1,j,0}$ 从 $i+1$ 走到 $i$ 来的，也可以从 $dp_{i+1,j,1}$ 从 $j$ 走到 $i$ 来的。那么这时所消耗的功耗就是 $a_1 + a_2 + \cdots + a_i$ 和 $a_{j+1} + \cdots + a_n$ 相加在乘上时间（也就是距离，用 $c$ 数组表示） $c_{i+1} - c_i$，如果我们用前缀和记录就是 $(s_n - s_j + s_i) \times (c_j - c_i)$。

$dp_{i,j,1}$ 同理，这边也就不过多赘述了。而然答案的话也很好猜，就是 $\min(dp_{1,n,0},dp_{1,n,1})$。

如果你看懂了，写出代码应该就不难了吧

### 3.3.2 代码

代码（已压行）：

```cpp

#include

using namespace std;

int a[110],b[110],s[110],dp[110][110][5];

int main(){

int n,t,sum=0;

cin>>n>>t;

for(int i=1;i<=n;i++)cin>>a[i]>>b[i],s[i]=s[i-1]+b[i];

memset(dp,0x3f,sizeof(dp));

dp[t][t][0]=dp[t][t][1]=0;

for(int l=2;l<=n;l++)for(int i=1;i<=n;i++){

int j=i+l-1;

dp[i][j][0]=min(dp[i+1][j][0]+(s[n]-s[j]+s[i])*(a[i+1]-a[i]),dp[i+1][j][1]+(s[n]-s[j]+s[i])*(a[j]-a[i]));

dp[i][j][1]=min(dp[i][j-1][1]+(s[n]-s[j-1]+s[i-1])*(a[j]-a[j-1]),dp[i][j-1][0]+(s[n]-s[j-1]+s[i-1])*(a[j]-a[i]));

}

cout<

return 0;

}

```

# 4.作业

1. T1：[P2858 [USACO06FEB] Treats for the Cows G/S](https://www.luogu.com.cn/problem/P2858)，难度：$2/5$。

2. T2：[P9325 [CCC 2023 S2] Symmetric Mountains](https://www.luogu.com.cn/problem/P9325)，难度：$2.5/5$。

3. [P3146 [USACO16OPEN] 248 G](https://www.luogu.com.cn/problem/P3146)，难度：$3/5$。

4. [P1063 [NOIP 2006 提高组] 能量项链](https://www.luogu.com.cn/problem/P1063)，难度：$3.5/5$。

5. [P4805 [CCC 2016] 合并饭团](https://www.luogu.com.cn/problem/P4805)，难度：$4/5$。

6. [P4302 [SCOI2003] 字符串折叠](https://www.luogu.com.cn/problem/P4302)，难度：$4.5/5$。

# 5.闲话

希望大家能喜欢我的文章，点个赞吧 QwQ

蒟蒻不才，膜拜大佬。如果文章有错字等问题，请在评论区@我。